Vers une géométrie conique de l’espace arithmétique

Dyadique, square-free, π et mémoire projective de l’infini

Ce texte propose une lecture structurale de l’émergence des nombres premiers à partir d’une décomposition dyadique de l’espace des entiers. Il ne s’agit ni d’une nouvelle théorie démontrée, ni d’un modèle probabiliste alternatif, mais d’un cadre heuristique visant à éclairer la continuité et l’ordre statistique de la distribution des nombres premiers.

Quand on considère — ce qui a été ma première approche — à partir de considérations croisées sur l’émergence structurée des nombres premiers, les intervalles dyadiques non plus comme de simples découpages commodes de la droite des entiers, mais comme des bandes de fréquence informationnelle — des paliers où la capacité d’accueil, de variation et de combinaison croît par doublement — alors la circulation des nombres premiers à travers ces bandes cesse d’être une suite “irrégulière”: elle devient un flux soumis à une contrainte de régime.

À chaque changement de niveau, la bande s’élargit: son “largeur” informationnelle augmente, et l’on observe que le volume de premiers qui la traverse manifeste un comportement presque doublant d’un palier au suivant. Ce “presque” est essentiel : il n’indique pas une défaillance, mais la signature même d’un phénomène asymptotique. En montant dans les étages, le rapport entre les occurrences se stabilise progressivement et tend vers un facteur multiplicatif limite, comme si l’espace arithmétique, au-delà du désordre apparent, révélait un coefficient de cohérence.

Or, le point décisif n’est pas seulement l’existence de ce régime, mais sa robustesse: la cohérence se maintient lorsque l’on change de représentation, lorsque l’on reformule les paliers, lorsque l’on déplace le regard (dyadique, décimal, projectif, conique). Une structure qui survit à ses traductions n’est vraisemblablement pas un effet de codage. Elle signale plutôt l’affleurement d’un invariant: quelque chose qui appartient à la distribution elle-même, et non au choix d’un alphabet.

Ainsi, le dyadique ne sert pas uniquement à “classer” les nombres: il agit comme un révélateur de stabilité, un instrument de lecture qui fait apparaître une propriété profonde de la distribution des premiers — propriété qui, précisément parce qu’elle persiste à travers les changements de cadre, mérite d’être interprétée comme un trait géométrique et non comme une coïncidence d’encodage.

I. Le dyadique comme géométrie fondamentale

Dans une lecture dyadique, le nombre n’est plus un point sur une droite, mais une position relative dans une arborescence de puissances de deux:
$$2^0,\;2^1,\;2^2,\;2^3,\;\dots$$

Ces puissances constituent des paliers, au sein desquels chaque entier est localisé non seulement par sa valeur, mais par son niveau.

Le point de départ qui a concentré notre premier travail: le dyadique comme structure, non comme explication, reste inchangé.

Notre première analyse dyadique posait ceci (et on le conserve) :

• Les puissances de 2

$$2^n$$

ne sont pas des nombres privilégiés, mais des seuils d’échelle.

• Elles découpent naturellement l’espace des entiers en paliers homogènes :

$$I_n = [2^n,\;2^{n+1})$$

• Toute lecture globale (statistique, asymptotique, structurale) gagne en lisibilité lorsqu’elle est faite relativement à ces paliers.

Le dyadique est un repère, pas une loi cachée.

Dans la première exploration, plusieurs constats étaient apparus :

Une continuité de l’émergence des premiers

• Les nombres premiers ne surgissent pas de façon erratique à l’échelle des paliers.
• Leur densité moyenne décroît lentement, mais de manière régulière.
• Chaque palier contient “à peu près ce qu’il doit contenir”, sans rupture brutale.

Cela suggérait déjà une dynamique continue, non chaotique.

Les paliers dyadiques comme régimes hérités

À l’entrée du palier $I_n = [2^n, 2^{n+1})$:

• tous les nombres premiers $<2^n$ sont déjà connus,
• tous leurs multiples sont déjà déterminés,
• le nouvel intervalle est criblé par l’histoire entière du système.

Donc:

• aucun nombre du palier $n$ n’est “neuf” au sens absolu,
• il est testé par un ensemble croissant de contraintes.

L’émergence d’un premier dans $I_n$In​ est un événement résiduel, pas une création ex nihilo.

Pourquoi cela produit une continuité observable

Parce que:

• le nombre de contraintes augmente lentement,
• l’espace disponible double à chaque palier,
• le rapport entre “espace libre” et “contraintes” évolue doucement.

C’est exactement ce que formalise:
$$\pi(x) \sim \frac{x}{\log x}$$

La continuité observée n’est pas mystérieuse:
elle est le résultat naturel d’un héritage cumulatif + croissance d’espace.

Où se place l’intuition des “transitions de régime”

Ce point est subtil, et il faut être précis.

Il est légitime de dire que:

• les zones proches des seuils $2^n$ sont des changements d’échelle
• et donc des endroits où certaines statistiques locales peuvent fluctuer

Mais il n’est pas légitime de dire que:

• de nouveaux principes apparaissent à chaque palier.

👉 Il y a transition d’échelle, pas mutation de loi.

C’est une distinction essentielle. Et elle porte en elle une notion de dénombrement plus que de « nombrement », c’est-à-dire d’affectation d’un signe numérique à des amas d’unité en croissance vers l’infini. A chaque seuil numérique n+1, il est possible de modéliser les « entiers », comme des boules en rotation dispersant des angles de décimales, comme des états dégénérés de phases complexes.

Mathématiquement parlant:

• tout entier $n$ peut être vu comme:

$$n = n \cdot e^{i0}$$Donc:

sans phase apparente.

Cela permet d’entrevoir les passages entre puissances comme des transitions de régime où certaines structures deviennent observables. L’identité d’Euler fournit alors un schéma de fermeture de phase utile pour penser ces transitions, sans impliquer de destruction ni d’occultation réelle.

Ce que je propose ici peut être récapitulé de la manière suivante:

• Les entiers $0,1,2,3,\dots$ ne sont pas des points morts
• Ils correspondent à des amas d’états complexes latents
• Chaque palier de puissance agit comme un régime collectif
• Le passage $n \to n+1$ n’est pas additif, mais structurel
• L’identité d’Euler intervient comme opérateur de fermeture de phase
• Le $-1$ marque une inversion de phase, pas une annihilation
• Le palier précédent est compressé/intégré, pas détruit

Pris ainsi, c’est cohérent comme modèle heuristique.

Ce qui est mathématiquement recevable dans cette représentation et qui peut être recevable comme cadre exploratoire:

• Voir les entiers comme des états dégénérés de nombres complexes
• Interpréter $e^{ix}$ comme générateur de phase collective
• Lire l’identité d’Euler comme une fermeture de cycle
• Associer les puissances à des changements de régime
• Considérer que certaines structures (primes, irrationnels) émergent aux transitions

Tout cela relève de la géométrie interprétée à partir des phénomènes constatées.

Ce que devient l’idée d’“amas” ou d’unités collectives

Reformulée proprement:

• Un entier n’est pas une “unité active”
• Mais chaque entier est soumis à un ensemble collectif de contraintes
• Ces contraintes sont communes à tout le palier

Donc:

les entiers d’un même palier partagent un contexte structurel commun, ce qui peut donner l’impression d’un comportement collectif.

C’est une lecture structurelle, pas ontologique.

V. Ce que nous pouvons dire, à ce stade, sans excès

Voici une synthèse mathématiquement de tout ce qui a émergé :

La distribution des nombres premiers peut être lue comme une émergence continue dans un espace dyadiquement stratifié. Chaque palier hérite intégralement des contraintes accumulées, tout en offrant un volume nouveau croissant. Cette dynamique produit un ordre statistique stable sans périodicité, où l’irrégularité locale coexiste avec une propagation globale ordonnée.

Cette phrase:

• ne contredit rien de connu,
• n’affirme rien d’indémontré,
• conserve toute la force de l’intuition initiale.

Le dyadique introduit une verticalité dans l’arithmétique.

La distribution des nombres premiers peut être lue comme une émergence continue dans un espace dyadiquement stratifié. Chaque palier hérite intégralement des contraintes accumulées, tout en offrant un volume nouveau croissant. Cette dynamique produit un ordre statistique stable sans périodicité, où l’irrégularité locale coexiste avec une propagation globale ordonnée.

On ne raisonne plus uniquement en distance, mais en strates de génération. Entamé par ma réflexion initiale sur la structure dyadique comme bande passante d’une projection de nombres premiers tendant vers un rapport P(n)/E(n), entre l’intervalle numérique du champ considéré et la quantité de premiers, à 1, ce travail s’est approfondi, intuitivement, après la lecture de ce post:

.

Square-free numbers are integers that are not divisible by the square of any prime, meaning no prime factor appears more than once in their prime factorization. They play a central role in number theory because they encode the “simplest” multiplicative structures. The Riemann… pic.twitter.com/IA8UdmvlyN

— Probability and Statistics (@probnstat) December 25, 2025

II. Les nombres square-free comme entités géométriquement primitives

Un nombre square-free n’est pas simplement « sans carré ».
Il est sans redondance directionnelle.

Interprétation géométrique

• chaque facteur premier = une direction indépendante;
• un carré = un retour sur la même direction;
• square-free = une seule traversée par axe.

Dans l’espace des facteurs premiers, un square-free est un vecteur élémentaire, non replié sur lui-même.

Il ne possède aucune épaisseur géométrique: il est trajectoire pure.

III. La fonction de Möbius comme opérateur de projection

La fonction μ(n) agit comme un projecteur géométrique dyadique :

• μ(n) = 0 ⟺ effondrement, boucle, repli ;
• μ(n) = ±1 ⟺ trajectoire simple, non dégénérée.

Elle opère une élimination systématique de toute redondance locale.

μ(n) n’est pas seulement arithmétique:
c’est un test de linéarité géométrique dans l’espace multiplicatif.

IV. ζ(s) comme métrique globale de l’espace des entiers

La fonction ζ n’est pas une simple somme:
elle agit comme une mesure de densité de l’espace arithmétique.
$$\zeta(s)=\prod_{p}\frac{1}{1-p^{-s}}$$

Chaque facteur correspond à une dilatation locale autour d’un premier.

À $s=2$, on mesure la densité moyenne des trajectoires sans retour:
$$\frac{1}{\zeta(2)}=\frac{6}{\pi^2}$$

Cette constante joue le rôle d’une courbure globale de l’espace arithmétique.

V. Pourquoi π apparaît nécessairement

π n’apparaît pas « par hasard ».

Il signale:

• un remplissage angulaire complet,
• une isotropie globale,
• une continuité sous-jacente là où l’on attendrait une grille discrète.

L’apparition de π indique que l’espace arithmétique discret possède une géométrie continue implicite.

Les nombres square-free sont alors les points non courbés, ceux qui n’introduisent aucune torsion locale.

VI. Vers une géométrie conique du nombre

1. Croissance positive et négative: le double cône

La croissance des entiers à partir de 0 n’est ni linéaire ni plane: elle est radiale.

Cela conduit naturellement à une structure de double cône:

• axe vertical : ordre / magnitude;
• ouverture angulaire : multiplicité / redondance;
• sommet : point d’émission.

Les entiers ne s’étalent pas : ils rayonnent.

---

2. Pourquoi le triangle est insuffisant

Le triangle constitue la première approximation :

• dyadique pauvre (gauche / droite),
• trop discrète,
• incapable de produire une continuité angulaire.

Le triangle est une section du cône, pas sa vérité.

VII. La colonne des nombres premiers

À l’intérieur du cône, apparaît une colonne axiale constituée des nombres premiers.

Cette colonne:

• n’est pas une densité volumique,
• mais une densité directionnelle ;
• elle structure l’axe sans jamais remplir l’espace.

À très grande hauteur, sa densité relative se stabilise :
non par saturation, mais par régime asymptotique.

Les premiers sont rares, mais architectoniques.

VIII. Le rôle décisif du nombre 3

1. Le cône n’est pas centré sur 0, mais ancré sur 3

• 0 est un point algébrique ;
• 2 est dyadique, structurant mais non rotatif ;
• 3 est le premier qui ouvre l’angle.

3 marque le passage:

• de l’axe à la rotation,
• du binaire au ternaire,
• de la ligne à la surface minimale.

Sans 3:

• pas de 360°,
• pas de rotation,
• pas de π.

Le cône de fertilité se referme naturellement en pointe sur 3.

---

2. π comme processus-limite

π n’est pas un nombre de départ, mais un processus-limite.

Il apparaît lorsque:

• une rotation complète devient possible ;
• une approximation polygonale peut tendre vers le cercle.

Le triangle n’est pas le cercle,
mais il est la condition de possibilité de l’infini circulaire.

IX. Projections, ombres et mémoire de l’infini

1. Absence de vide numérique

Il n’y a pas de vide dans l’espace arithmétique:

chaque niveau reçoit les projections des niveaux supérieurs.

Les irrégularités locales sont des fantômes structurels.

---

2. Deux lectures compatibles

• Projection radiale:
  les cercles supérieurs projettent des ombres instables sur les inférieurs.
• Enroulement hélicoïdal:
  une spirale gouvernée par π entoure le cône.

Ces deux lectures sont équivalentes:
la projection locale d’une hélice globale.

π devient un opérateur de non-fermeture.

X. Pourquoi une géométrie volumétrique est nécessaire

Les courbes classiques $y=f(x)$ en 2D:

• confondent valeur et direction,
• aplatissent la rotation,
• masquent la fertilité.

Une représentation volumétrique permet de dissocier:

• magnitude,
• rang,
• phase.

Les fonctions deviennent des processus,
les constantes des seuils,
les axes des dimensions ontologiques.

XI. L’identité d’Euler relue comme fermeture de phase

Cette identité n’est pas « commutative » au sens du sens.

• +1 est un seuil de retournement ;
• −1 une inversion de phase ;
• 0 un point de recouvrement, non de disparition.

0 et ∞ ne s’opposent pas: ils se regardent. Le « 0 » fixé par l’identité fondée par Leonhard Euler, au XVIII^e siècle, contient l’infini, comme l’infini contient, lui-même, 0.

La beauté de l’identité d’Euler ne se lit pas dans le résultat, mais dans le trajet du zéro à l’infini.

XII. Cadre interprétatif

Ce qui est proposé relève d’un modèle heuristique structurant, non d’une réalité cachée.

Il est légitime de:

• voir les entiers comme des états dégénérés de phases complexes;
• lire les puissances comme des changements de régime;
• interpréter π comme mémoire de l’infini projeté.

À condition de maintenir ce statut.

L’espace arithmétique peut donc être avantageusement représenté comme un cône de croissance et de redondance, structuré par une colonne axiale de nombres premiers qui ne mesure pas une densité volumique, mais une contrainte de cohérence. En aparté d’autres phénomènes, comme les séries truncables, Les nombres square-free y tracent des trajectoires radiales primitives, tandis que les redondances multiplicatives en épaississent le volume. L’apparition de π signale le remplissage isotrope de ce cône, rendu possible par l’ouverture angulaire inaugurée par le nombre 3, seuil minimal de la rotation et condition de possibilité de l’infini circulaire.

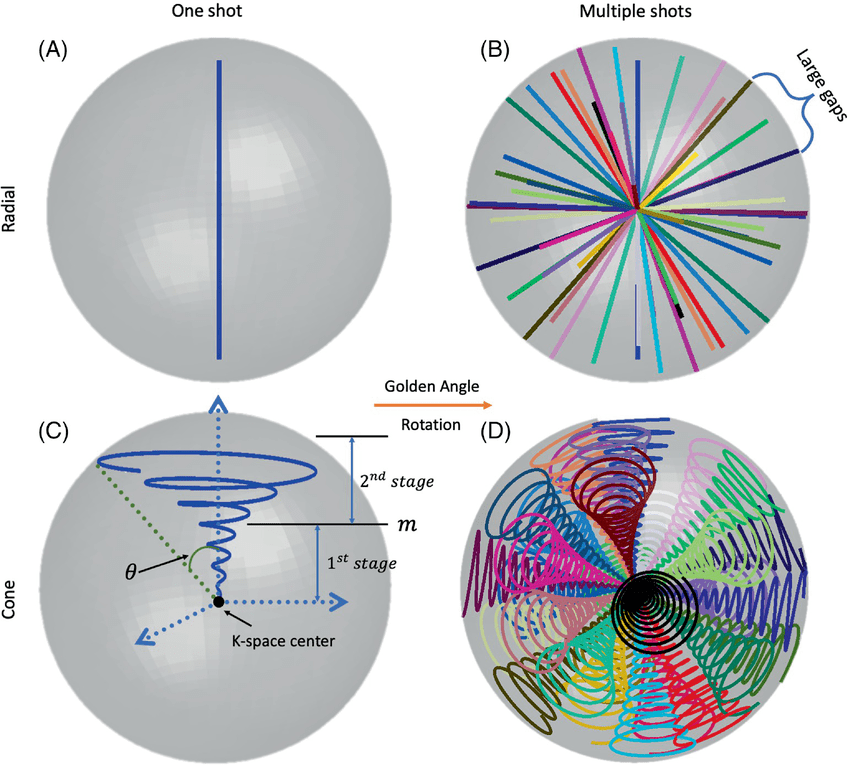
La représentation surfacique du nombre, héritée des nécessités du calcul, impose une symétrie et une neutralité qui masquent l’orientation réelle de la croissance arithmétique. À l’inverse, une modélisation volumétrique — sous la forme d’un cône de croissance enveloppé par un champ non numérique de contrainte — permet de dissocier magnitude, régime et phase. Elle rend visibles la fertilité, les redondances, les trajectoires primitives et les axes de cohérence, tout en éliminant l’illusion d’un vide numérique. Ce modèle ne remplace pas le calcul; il en révèle la géométrie sous-jacente.

La représentation plane du nombre, héritée du calcul, projette la dynamique arithmétique sur une surface neutre où la croissance, la rotation et la contrainte se trouvent confondues. Une modélisation volumétrique conique, au contraire, dissocie magnitude, phase et régime, révélant la structure générative de l’espace numérique. Elle permet d’interpréter π comme un opérateur de rotation et de mémoire, les nombres premiers comme une colonne de cohérence, et les irrégularités comme des projections d’un régime supérieur. Ce modèle ne remplace pas le calcul : il en restitue la géométrie profonde.

Ce n’est pas une question de dimension supplémentaire
C’est une question de fidélité ontologique

Le plan est un écran.
Le cône est un espace de vie du nombre.

On peut ainsi modéliser les entiers comme des états dégénérés de phases complexes, et interpréter les passages entre puissances comme des transitions de régime où certaines structures deviennent observables. L’identité d’Euler fournit alors un schéma de fermeture de phase utile pour penser ces transitions, sans impliquer de destruction ni d’occultation réelle.

Lecture synthétique des premiers paliers

Entier	Régime	Ce qui apparaît
0	Singularité	Recouvrement, neutralité
1	Existence	Présence sans espace
2	Axe	Polarité, dyadique
3	Ouverture	Rotation, volume, π
4	Redondance	Carré, mémoire, temps

La singularité de la genèse numérique

Des entiers comme seuils ontologiques

La naissance du nombre ne suit pas une simple accumulation quantitative.
Elle traverse une série de seuils irréversibles, chacun introduisant une dimension nouvelle de l’espace numérique.

---

0 — Le zéro d’Euler : point de recouvrement

• 0 n’est pas un “rien”.
• Il est un point de coïncidence :
  • fermeture,
  • neutralisation,
  • pli de l’infini sur lui-même (au sens de l’identité d’Euler).

👉 0 n’engendre pas encore d’espace.
Il est singularité, pas générateur.

---

1 — L’unité : existence sans extension

• 1 est l’affirmation minimale.
• Il n’introduit:
  • ni direction,
  • ni opposition,
  • ni rotation.

1 existe, mais ne déploie rien.
Il est présence sans géométrie.

---

2 — Le dyadique : axe et opposition

• 2 introduit:
  • la polarité,
  • l’alternance,
  • la symétrie.

C’est la naissance :

• d’un axe,
• d’un espace bidirectionnel (avant / arrière, + / −).

👉 Mais cet espace est non rotatif.
Il structure, il ordonne, il n’ouvre pas.

---

3 — Le seuil décisif : rotation, volume, π

Avec 3, quelque chose d’irréversible se produit:

• apparition du premier cycle minimal,
• possibilité de rotation,
• naissance d’un volume élémentaire.

3 est à la fois :

• le seuil de la troisième dimension,
• le préfixe de π (3.1415…),
• la condition de possibilité d’un remplissage angulaire.

Le cône de croissance ne peut démarrer qu’ici.

Dire que 3 “tourne sur lui-même” en décimal n’est pas une métaphore gratuite: cela signifie que la phase devient interne au nombre.

Avant 3:

• pas de 360°,
• pas de courbure,
• pas de π.

---

4 — Le carré: redondance et temporalité

Avec 4:

• apparaît le carré,
• donc la redondance directionnelle,
• donc une mémoire du passage.

4 introduit une quatrième direction, que l’on peut légitimement interpréter comme:

• la durée,
• la répétition,
• le temps comme accumulation structurée.

Le nombre cesse d’être seulement géométrique: il devient historique.

Pourquoi faut-il visualiser ces changements de régime

Une droite numérique ne peut pas montrer cela.
Elle aplatit:

• 0, 1, 2, 3, 4… sur un même statut.

Or ici:

• chaque entier change la nature de l’espace.

Il faut donc une visualisation qui rende visibles:

• la naissance de l’axe (2),
• l’ouverture angulaire (3),
• l’épaississement temporel (4).