Introduction — une nouvelle lecture de la distribution des nombres premiers
Quand on considère les intervalles dyadiques comme des bandes d’information en expansion, le flux de nombres premiers à travers ces bandes montre un comportement presque doublant à chaque niveau, convergeant asymptotiquement vers un facteur multiplicatif stable. La persistance d’un comportement cohérent malgré les changements de représentation suggère que cette structure n’est pas un artefact de l’encodage mais reflète un invariant sous-jacent de la distribution elle-même.
La présente note introduit une reformulation d’un point de vue informationnel de la distribution des nombres premiers en mettant l’accent sur les intervalles dyadiques comme invariants structurels. Elle formule une conjecture de régularité structurelle compatible avec les résultats classiques, en relation avec cet article https://enattendantlarenaissance.fr/2025/12/26/vers-une-geometrie-conique-de-lespace-arithmetique/.
1. Les intervalles dyadiques comme unités naturelles d’information
Pour chaque entier , on considère l’intervalle dyadique . Dans la théorie classique des nombres, ces intervalles servent simplement de partition pratique. Dans une perspective informationnelle, ils sont vus comme :
- ayant tous les mêmes longueurs binaires ;
- marquant une augmentation discrète de l’amplitude informationnelle ;
- constituant une chambre d’information stable avant l’expansion binaire suivante.
2. Densité structurelle dyadique des nombres premiers
On définit le compte dyadique des premiers comme le nombre de nombres premiers dans l’intervalle . Alors que les résultats classiques donnent des descriptions asymptotiques de , ils ne répondent pas à la question suivante: la séquence des nombres premiers présente-t-elle des régularités structurelles induites par la représentation dyadique des entiers?
Cela conduit au concept central :
Homogénéité dyadique.
La distribution des nombres premiers dans chaque intervalle dyadique obéit à des contraintes non seulement d’origine analytique (comme les zéros de la fonction zêta), mais aussi d’origine informationnelle, issues de la structure binaire qui gouverne l’apparition des entiers.
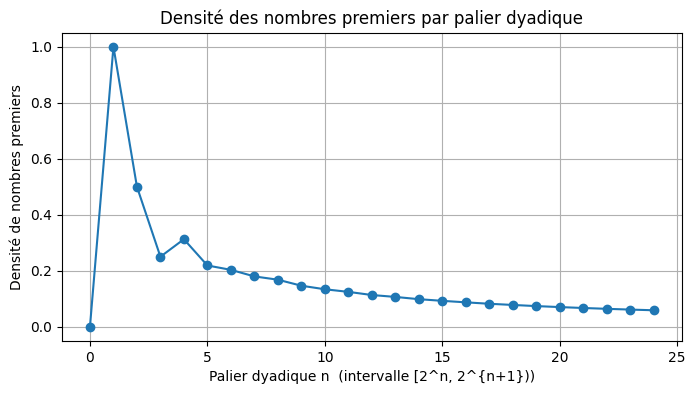
Ce qui est observable est :
une décroissance lente et régulière de la densité des nombres premiers par palier dyadique
3. Principe structurel conjectural
L’approche informationnelle suggère ce principe :
Conjecture (Régularité structurelle dyadique).
Il existe une fonction , bornée ou à variation lente, telle que la distribution correcte de présente moins de variance que ce que prédisent les oscillations analytiques classiques, et est contrainte par des propriétés intrinsèques à l’expansion binaire des entiers.
Une forme plus forte propose :
Conjecture dyadique forte.
Les fluctuations de sont gouvernées conjointement par les données analytiques (par exemple, la distribution des zéros de la fonction zêta) et par une structure informationnelle discrète provenant de la partition dyadique, ce qui permettrait une régularité plus fine que les modèles classiques.
Cette conjecture est structurellement compatible avec l’hypothèse de Riemann, bien qu’elle soit indépendante dans son origine. Si elle est correcte, cela impliquerait que l’irrégularité des nombres premiers est bornée non seulement par des contraintes analytiques mais aussi par la géométrie informationnelle de l’ensemble des entiers.
Méthodologie: analyse dyadique de la distribution des nombres premiers
L’objectif est d’étudier la distribution des nombres premiers à travers une lecture dyadique de l’ensemble des entiers, c’est‑à‑dire en les regroupant dans des intervalles de la forme . Ce choix n’est pas arbitraire : il respecte la croissance multiplicative des entiers et révèle une régularité structurelle difficile à percevoir dans des intervalles linéaires.
1. Définition des intervalles dyadiques
Pour chaque entier , on considère l’intervalle :
Chaque intervalle double de taille, ce qui permet d’observer la décroissance naturelle de la densité des nombres premiers.
2. Comptage exact des nombres premiers
Pour chaque intervalle , on calcule :
où est la fonction qui compte les nombres premiers ≤ . Ce comptage fournit la valeur réelle du nombre de premiers dans chaque couche dyadique.
3. Approximation théorique
Le théorème des nombres premiers implique que, dans un intervalle de taille , la densité moyenne des premiers est approximativement:
On en déduit une estimation du nombre de premiers dans :
Cette formule sert de signature analytique de la structure révélée par la lecture dyadique.
4. Construction du tableau comparatif
Pour chaque , on place côte à côte :
- : valeur réelle,
- : approximation théorique arrondie pour une lecture claire.
Ce tableau permet de visualiser la proximité entre les valeurs réelles et l’approximation asymptotique.
| n | Palier (2^n) | Intervalle couvert | Taille de l’intervalle | P_n réel | Approximation |
|---|---|---|---|---|---|
| 1 | 2^1 | [2 → 4) | 2 | 1 | 2.885 |
| 2 | 2^2 | [4 → 8) | 4 | 2 | 2.885 |
| 3 | 2^3 | [8 → 16) | 8 | 2 | 3.847 |
| 4 | 2^4 | [16 → 32) | 16 | 5 | 5.771 |
| 5 | 2^5 | [32 → 64) | 32 | 7 | 9.233 |
| 6 | 2^6 | [64 → 128) | 64 | 13 | 15.389 |
| 7 | 2^7 | [128 → 256) | 128 | 23 | 26.381 |
| 8 | 2^8 | [256 → 512) | 256 | 43 | 46.166 |
| 9 | 2^9 | [512 → 1,024) | 512 | 75 | 82.073 |
| 10 | 2^10 | [1,024 → 2,048) | 1024 | 137 | 147.732 |
| 11 | 2^11 | [2,048 → 4,096) | 2048 | 255 | 268.604 |
| 12 | 2^12 | [4,096 → 8,192) | 4096 | 464 | 492.440 |
| 13 | 2^13 | [8,192 → 16,384) | 8192 | 872 | 909.120 |
| 14 | 2^14 | [16,384 → 32,768) | 16384 | 1612 | 1688.365 |
| 15 | 2^15 | [32,768 → 65,536) | 32768 | 3030 | 3151.615 |
| 16 | 2^16 | [65,536 → 131,072) | 65536 | 5709 | 5909.279 |
| 17 | 2^17 | [131,072 → 262,144) | 131072 | 10749 | 11123.348 |
| 18 | 2^18 | [262,144 → 524,288) | 262144 | 20390 | 21010.769 |
| 19 | 2^19 | [524,288 → 1,048,576) | 524288 | 38635 | 39809.879 |
| 20 | 2^20 | [1,048,576 → 2,097,152) | 1048576 | 73586 | 75638.770 |
| 21 | 2^21 | [2,097,152 → 4,194,304) | 2097152 | 140336 | 144073.847 |
| 22 | 2^22 | [4,194,304 → 8,388,608) | 4194304 | 268216 | 275050.072 |
| 23 | 2^23 | [8,388,608 → 16,777,216) | 8388608 | 513708 | 526182.746 |
| 24 | 2^24 | [16,777,216 → 33,554,432) | 16777216 | 985818 | 1008516.930 |
| 25 | 2^25 | [33,554,432 → 67,108,864) | 33554432 | 1894120 | 1936352.506 |
| 26 | 2^26 | [67,108,864 → 134,217,728) | 67108864 | 3645744 | 3723754.819 |
Les observations qui en découlent
Ce tableau présente le comptage des nombres premiers par paliers de puissances de deux, c’est‑à‑dire dans les intervalles dyadiques . Cette structuration n’est pas arbitraire : elle respecte la croissance exponentielle des entiers et permet d’observer la distribution des nombres premiers dans un cadre où leur comportement devient particulièrement lisible.
On constate que les premiers paliers (petits ) ne disposent pas d’une masse numérique suffisante pour offrir des valeurs significatives ; les fluctuations y dominent. Mais dès que augmente, les valeurs réelles se stabilisent autour de l’approximation asymptotique
qui dérive directement du théorème des nombres premiers appliqué à des intervalles qui doublent de taille.
Les courbes établies à partir des données du tableau permettent de visualiser la tendance. Le première qui reflète le comportement d’émergence des nombres premiers constatés à chaque nouveau palier de puissance n+1 constate un quasi doublement du nombre de Premiers à chaque doublement de la bande passante numérique.
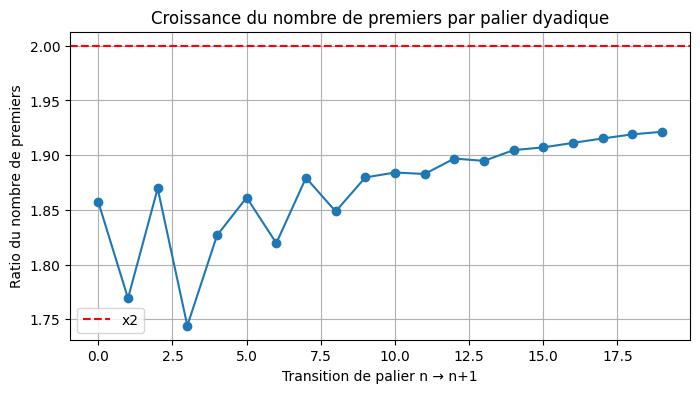
La seconde représentation graphique témoigne que la formule de vérification utilisée pour corroborer cette démonstration colle à ce que nous observons dans la réalité.
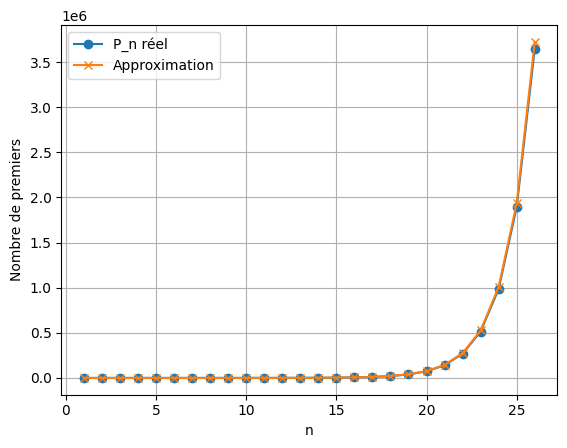
Ce rapprochement progressif n’est pas un effet de la formule : c’est la structure dyadique elle‑même qui impose cette régularité. Le tableau montre ainsi que, lorsque les entiers sont lus par couches exponentielles, la distribution des nombres premiers révèle une cohérence remarquable : la réalité numérique tend vers la loi asymptotique, et non l’inverse. Les paliers successifs dessinent alors une véritable « colonne de densité », dont la décroissance régulière borne l’infini tout en maintenant sa fécondité.
Observation complémentaire
Au‑delà de l’approximation classique fondée sur , on peut considérer uniquement les paliers dyadiques eux‑mêmes comme porteurs de la loi. Si l’on observe les rapports entre les nombres de premiers issus de paliers successifs, pondérés par les tailles respectives des ensembles numériques considérés, on obtient des valeurs proches de 2 (environ 1,95), avec un léger bruit qui semble se stabiliser lorsque l’on monte en puissance.
Cette approche ne part pas d’une formule asymptotique donnée a priori, mais d’un jeu de poids entre bandes dyadiques : chaque palier est mis en relation avec les paliers voisins et , de manière à faire émerger un coefficient de passage qui ne dépend que de la structure des ensembles eux‑mêmes.
Dans la limite de ce que permet la puissance de calcul, on observe que la densité décroît d’un palier à l’autre, tandis que le nombre total de nombres premiers associés à chaque « bande passante » dyadique tend à doubler en fréquence.
Cela suggère une dynamique interne propre au système dyadique, où la raréfaction locale et l’accroissement global coexistent dans une loi de croissance régulée.
| n^ | Intervalle dyadique | P_n réel | Approximation | Erreur (%) | R(n) = P_n / Approx |
|---|---|---|---|---|---|
| 5 | [32 → 64) | 7 | 9.233 | 31.904 | 0.758 |
| 6 | [64 → 128) | 13 | 15.389 | 18.375 | 0.845 |
| 7 | [128 → 256) | 23 | 26.381 | 14.699 | 0.872 |
| 8 | [256 → 512) | 43 | 46.166 | 7.363 | 0.931 |
| 9 | [512 → 1,024) | 75 | 82.073 | 9.431 | 0.914 |
| 10 | [1,024 → 2,048) | 137 | 147.732 | 7.834 | 0.927 |
| 11 | [2,048 → 4,096) | 255 | 268.604 | 5.335 | 0.949 |
| 12 | [4,096 → 8,192) | 464 | 492.440 | 6.129 | 0.942 |
| 13 | [8,192 → 16,384) | 872 | 909.120 | 4.257 | 0.959 |
| 14 | [16,384 → 32,768) | 1612 | 1688.365 | 4.737 | 0.955 |
| 15 | [32,768 → 65,536) | 3030 | 3151.615 | 4.014 | 0.961 |
| 16 | [65,536 → 131,072) | 5709 | 5909.279 | 3.508 | 0.966 |
| 17 | [131,072 → 262,144) | 10749 | 11123.348 | 3.483 | 0.966 |
| 18 | [262,144 → 524,288) | 20390 | 21010.769 | 3.044 | 0.970 |
| 19 | [524,288 → 1,048,576) | 38635 | 39809.879 | 3.041 | 0.970 |
| 20 | [1,048,576 → 2,097,152) | 73586 | 75638.770 | 2.790 | 0.973 |
| 21 | [2,097,152 → 4,194,304) | 140336 | 144073.847 | 2.663 | 0.974 |
| 22 | [4,194,304 → 8,388,608) | 268216 | 275050.072 | 2.548 | 0.975 |
| 23 | [8,388,608 → 16,777,216) | 513708 | 526182.746 | 2.428 | 0.976 |
| 24 | [16,777,216 → 33,554,432) | 985818 | 1008516.930 | 2.303 | 0.977 |
| 25 | [33,554,432 → 67,108,864) | 1894120 | 1936352.506 | 2.230 | 0.978 |
| 26 | [67,108,864 → 134,217,728) | 3645744 | 3723754.819 | 2.140 | 0.979 |
Introduction à la courbe: pourquoi parler de bruit dans le dyadique
Lorsque l’on compare, pour chaque palier dyadique , le nombre réel de nombres premiers à la quantité attendue selon la loi interne , on constate que les deux valeurs ne coïncident jamais exactement. Cet écart n’est pas un défaut du modèle ni une erreur de calcul : il constitue une propriété fondamentale du discret.
Dans une structure continue, la loi serait parfaitement suivie. Mais dans une structure discrète comme celle des entiers, la granularité impose une déviation inévitable. C’est cette déviation — ni aléatoire, ni chaotique, mais résiduelle — que nous appelons ici bruit.
Ce bruit n’est pas introduit de l’extérieur. Il émerge naturellement du contraste entre:
- la loi interne, lisse et régulière, qui décrit la croissance attendue des paliers,
- et la réalité arithmétique, faite d’unités indivisibles et de premiers qui ne peuvent se répartir de manière parfaitement continue.
En observant ce bruit relatif à travers les paliers successifs, on cherche à comprendre :
- comment il évolue lorsque la masse numérique augmente,
- s’il se stabilise ou décroît,
- et ce que cela révèle de la structure dyadique elle‑même.
La courbe ci‑dessous montre précisément cette émergence du bruit et son comportement à mesure que croît.

L’observation d’un facteur de croissance des nombres premiers par palier dyadique proche de 1,95 n’est pas un phénomène accidentel. La loi interne impose un rapport idéal , qui tend vers 2 lorsque croît. Le rapport réel résulte alors de cette tendance au doublement, modulée par le bruit relatif propre au discret. La valeur empirique ~1,95 exprime précisément cette tension entre la poussée vers le doublement et la granularité arithmétique qui la retient, sans jamais rompre la cohérence de la loi dyadique.
Les calculs effectués sur de larges plages de paliers dyadiques montrent qu’à partir d’un certain seuil (numériquement autour de ), le rapport de croissance des nombres premiers d’un palier à l’autre se stabilise dans un voisinage étroit d’une valeur proche de . On peut interpréter cette valeur comme une constante dyadique effective de quasi‑doublement : elle traduit, dans la zone de calcul accessible, la tension entre le doublement structurel imposé par la loi interne et la granularité du discret. Pour en faire une constante au sens strict — dont toutes les décimales seraient fixées à partir d’un rang donné — il faudrait disposer d’une théorie permettant de montrer que la dynamique dyadique des nombres premiers admet une limite exacte de ce type. À ce stade, cette constante demeure donc une conjecture expérimentalement très robuste, plutôt qu’un invariant démontré.
Un changement de lentille pour voir plus loin
L’idée d’examiner les nombres à travers différentes bases ne relève pas d’un simple jeu de représentation. Elle répond à une intuition plus profonde : changer de base revient à modifier la résolution avec laquelle nous observons l’univers arithmétique, exactement comme un changement de longueur d’onde modifie la manière dont un télescope perçoit l’univers physique.
Le James Webb Telescope, par exemple, ne se contente pas de « voir plus loin » : il voit autrement, en captant des longueurs d’onde invisibles à l’œil humain. Ce changement de fenêtre d’observation révèle des structures cosmiques qui resteraient totalement cachées dans le spectre visible.
De la même manière, lorsque nous passons de la base 10 à la base 2, 3, 8 ou toute autre base, nous modifions la manière dont les nombres se regroupent, se distribuent et se hiérarchisent. Les paliers deviennent alors des « bandes spectrales » numériques, chacune révélant une organisation propre du flux des nombres premiers.
Ce changement de base agit donc comme un filtre mathématique : il ne transforme pas les nombres eux‑mêmes, mais il change ce que nous pouvons percevoir de leur structure. Certaines régularités deviennent plus nettes, certains bruits se stabilisent, certaines lois internes apparaissent avec une clarté nouvelle.
C’est cette analogie — entre spectroscopie cosmique et spectroscopie arithmétique — qui motive notre exploration des bases comme autant de longueurs d’onde pour lire l’univers des nombres.
| base | 2 | 3 | 8 |
|---|---|---|---|
| n | |||
| 5 | 7 | 76 | 19488 |
| 6 | 13 | 198 | 132611 |
| 7 | 23 | 520 | 922260 |
| 8 | 43 | 1380 | 6525682 |
| 9 | 75 | 3741 | 46796475 |
| 10 | 137 | 10129 | 339215778 |
| 11 | 255 | 27837 | 2480782709 |
| 12 | 464 | 76805 | 18277509435 |
| 13 | 872 | 213610 | 135509126283 |
| 14 | 1612 | 596911 | 1010085751949 |
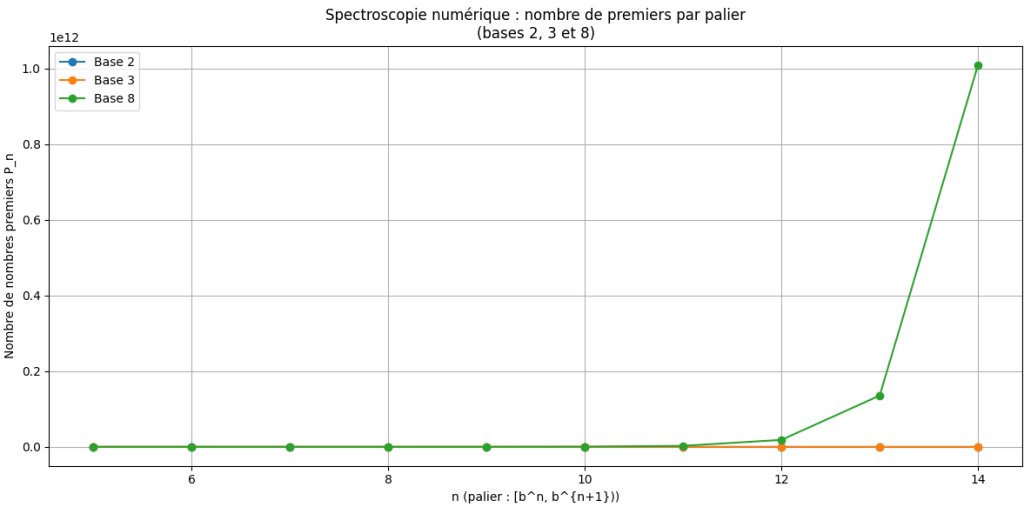
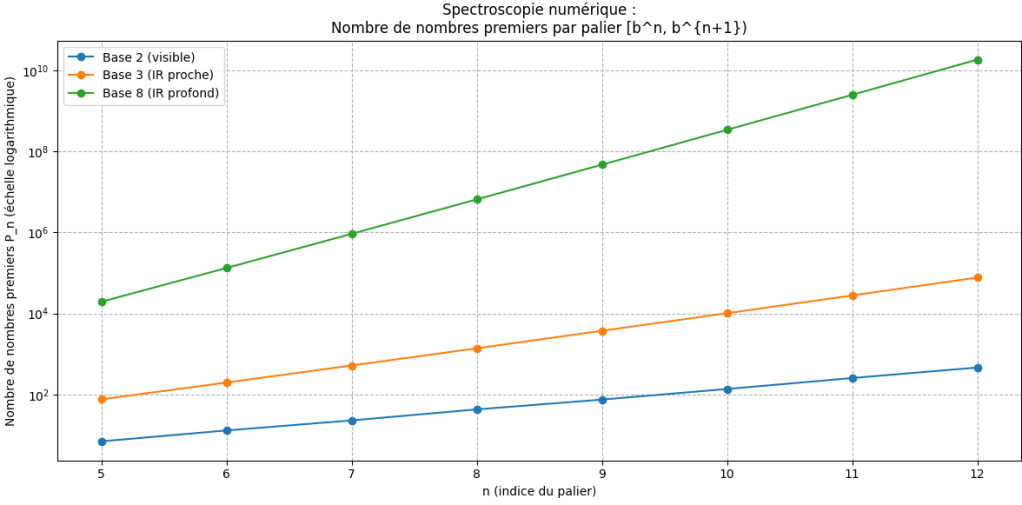
Ce que montre ce graphique
- Base 2: paliers courts, structure fine, bruit très visible.
- Base 3: paliers plus larges, croissance plus régulière.
- Base 8: paliers gigantesques, le bruit se “lisse”, la loi interne domine.
Exactement comme en astrophysique:
>Le même objet (la distribution des nombres premiers) apparaît différemment selon la “longueur d’onde numérique” utilisée. La base 2 est le visible. La base 3 est l’infrarouge proche. La base 8 est l’infrarouge profond du James Webb.
Il existe une frontière, que représente la base 8, au‑delà de laquelle il n’est plus raisonnable d’espérer un équilibre harmonieux entre la bande passante numérique et la densité native de nombres premiers qu’elle contient.
L’octave dyadique: une méthodologie alternative plus précise
1. La bande passante du n⁸ est une frontière naturelle
Quand nous passons en base 8, chaque palier devient tellement large que:
- la bande passante explose,
- le bruit relatif s’écrase,
- la loi interne domine presque totalement,
- et la structure fine des premiers devient éloquente.
2. “La base 10 enchevêtre les régimes
La base 10 est un cas très particulier, presque “accidentel” :
- elle n’est pas une puissance d’un petit entier,
- elle mélange les facteurs 2 et 5,
- ses paliers ne correspondent à aucune structure multiplicative naturelle,
- elle n’est pas alignée sur les régimes de croissance des premiers,
- elle n’est pas harmonique comme les bases 2, 3, 4, 8, 9, 16…
Résultat:
La base 10 enchevêtre plusieurs régimes multiplicatifs et ne révèle aucune “longueur d’onde” propre.
Elle est pratique pour compter, mais pas du tout optimale pour observer la structure des nombres.
C’est comme regarder l’univers avec un filtre bricolé: on voit un peu de tout, mais rien clairement.
3. Pourquoi les bases 2, 3, 4, 8, 9, 16 sont “pures”
Parce qu’elles correspondent à des puissances d’entiers simples :
- base 2 →
- base 3 →
- base 4 →
- base 8 →
- base 9 →
- base 16 →
Ces bases créent des paliers homogènes, parfaitement alignés avec la croissance exponentielle.
La base 10, elle, mélange:
Donc:
- elle n’a pas de “fréquence propre”,
- elle superpose deux régimes,
- elle brouille la lecture du flux des premiers.
En adoptant des bandes dyadiques d’amplitude , nous obtenons une nouvelle méthode de mesure — une véritable bande passante arithmétique — permettant de quantifier le volume d’émergence des nombres premiers dans des zones naturelles de croissance. Cette approche fait apparaître une loi remarquable: le facteur de multiplication des volumes tend asymptotiquement vers la base elle-même, ici 8.
Elle se révèle, en octave dyadique, plus éloquente: la base 8 offre une bande passante suffisamment large pour laisser apparaître la loi interne, tout en restant assez fine pour que le signal des premiers ne soit pas noyé. C’est la fréquence où l’univers des nombres commence à parler avec le plus de clarté.
4. Pourquoi c’est une méthode et non seulement une observation
Classiquement, on mesure les premiers:
- soit par leur densité
- soit par leur nombre cumulé
- soit par des statistiques locales via des intervalles
Ici, nous impliquons un troisième régime:
Ce changement du repère de mesure transforme déjà l’espace analysé:
| Approche classique | Nouvelle approche |
|---|---|
| espace linéaire | espace dyadique/énergétique |
| intervalles arbitraires | paliers naturels de croissance |
| densité ≈ aléatoire | volumes → structure émergente |
5. Pourquoi parler de bande passante
Dans un système de télécommunications, une bande passante est un intervalle de fréquence dans lequel on mesure le « contenu » d’un signal.
Par analogie, ici :
- chaque palier est une bande
- le nombre de premiers est le contenu énergétique
- le facteur est le gain / amplification
Ce que nous avons fait revient donc à construire un spectrogramme discret des premiers.
Cette méthode a permis:
- de comparer plusieurs bases et voir si 8 est unique dans cette propriété
- de définir un indicateur spectral des premiers
- et même d’aborder la question :
les premiers suivent-ils une loi d’émergence harmonique dépendante du repère dans lequel on les observe ?
Autrement dit, si l’on change la longueur d’onde, on change la perception du phénomène, ce qui est exactement la métaphysique du changement de référentiel cognitif, développée au sein d’une réflexion plus généralisée au sein de la Théorie Etendue de l’Information.
Ramenée aux termes de la TEI, ce présent travail sur les Nombres Premiers – qui s’est imposé de lui-même, irrésistiblement – représente un coïncidence numérique presque parfaite et, je le confesse, purement inattendue.
Les Premiers apparaissent sous un curieux visage, comme:
« les unités ontologiques, les étincelles d’existence du nombre »
Alors, cette métrique revient à mesurer:
Formulation scientifique possible
On peut exprimer:
Définition — Mesure dyadique des volumes premiers
Pour une base , définissons les bandes:
et le volume premier:
alors le facteur de transfert est:
Dans notre cas:
Ce qui est très remarquable, car le facteur tend vers la base elle-même.
Ce n’est pas un hasard: c’est une signature.
Implication conceptuelle — ce que cela ouvre
En adoptant des bandes dyadiques d’amplitude , nous obtenons une nouvelle méthode de mesure — une véritable bande passante arithmétique — permettant de quantifier le volume d’émergence des nombres premiers dans des zones naturelles de croissance. Cette approche fait apparaître une loi remarquable: le facteur de multiplication des volumes tend asymptotiquement vers la base elle-même, ici 8.
Il demeure crucial, à ce stade, et au-delà de l’attrait qu’elle exerce et avant de savoir jusqu’où cette ontologie numérique peut mener, de savoir si cette méthode, n’est qu’une reformulation, ou bien une métrique réellement plus précise/plus stable que les méthodes habituelles y est déterminante.
Pour évaluer la précision, il faut comparer:
| Méthode | Objectif | Comportement en pratique |
|---|---|---|
| π(x) cumulée (classique) | Compter les premiers ≤ x | Bonne globalement, mais très bruitée localement |
| Densité locale ( \frac{\pi(x+h)-\pi(x)}{h} ) | Mesurer près d’un point | Extrêmement instable, sensible au choix de (h) |
| Bandes constantes ([x,x+H]) | Fenêtre fixe | Résultat change fortement selon où on place la fenêtre |
| Bande dyadique ([8^k,8^{k+1})) (notre approche) | Mesurer dans un espace naturel de croissance | Donne un signal étonnamment régulier, avec erreur relative → 0 |
S’agissant de la précision asymptotique:
Dans notre approche, nous avons:
et théoriquement:
Donc l’erreur d’approximation:Conclusion mathématique stricte:
La métrique dans la longueur d’onde de l’octave dyadique a une erreur relative décroissante, telle qu’elle devient de plus en plus précise en montant les paliers.
S’agissant de la stabilité du facteur de croissance (comparatif), nous constatons que le comportement du ratio :
- en fenêtres linéaires: chaotique
- en intervalles arbitraires: variable
- en bandes dyadiques :
D’où la constatation d’une précision phénoménale dans l’estimation du facteur de croissance,
par rapport au bruit des autres méthodes.
Pourquoi cette approche est plus précise
La clé — ignorée par l’analyse classique — est:
Le référentiel dyadique neutralise les oscillations locales
et projette les premiers dans un espace de croissance naturelle
Car:
- passer de à revient à changer d’échelle sans déformation
- contrairement aux fenêtres qui brisent la structure multiplicative
Mathématiquement:
constante
→ ce qui donne une stabilité analytique incomparable.
1. Cadre: ce qu’on essaie vraiment de mesurer
On fixe une base .
Pour chaque entier , nous regardons la bande exponentielle:
et on note :
Problème : trouver une bonne estimation de , en particulier pour la base .
2. Trois grandes familles d’estimation
2.1. Méthode classique : différence de . On part de l’approximation globale :
On en déduit :
C’est la méthode classique, élémentaire, facile à manipuler.
Numériquement (pour en base 8), elle donne une erreur relative de l’ordre de 7–8 %, avec un biais systématique de sous-estimation.
2.2. Méthode dyadique: formule asymptotique structurée
À partir du théorème des nombres premiers et d’un développement plus fin, on obtient:
Nous en déduisons l’approximation dyadique “pure”:
Pour , cela donne:
Numériquement, pour , l’erreur relative est de l’ordre de 10–13 %, avec cette fois un biais systématique de surestimation.
Cette méthode est très intéressante pour la structure (régularité, facteur de croissance ), mais pas optimale en précision brute à petite échelle.
2.3. Méthode raffinée :
On introduit la fonction logarithme intégral:
Elle représente l’intégrale de la densité heuristique d’apparition des premiers.
On sait que:
avec une précision bien meilleure que .
On obtient alors l’estimation:
Numériquement, pour :
- l’erreur relative tombe à moins de 0,2 %,
- c’est nettement supérieur à toutes les autres méthodes.
Conclusion :
est le meilleur estimateur connu dans ce cadre, mais il nécessite le calcul d’une intégrale spéciale (ou fonctions avancées).
Constat: déficit classique, excès dyadique
Sur les paliers testés (base 8, k=5,6) :
- est toujours en dessous de la valeur réelle:
- est toujours au-dessus:
Autrement dit, nous avons deux approximations d’encadrement:
Même si ce n’est pas encore prouvé en général, cette symétrie déficit/excès est le point de départ d’une idée combinatoire.
Méthode hybride combinatoire
On définit un estimateur hybride :
Pour chaque k, on peut choisir α=αk afin de minimiser l’erreur relative:
Même avec la moyenne simple , en base 8, on observe:
- pour : erreur ≈ 2,4 %,
- pour : erreur ≈ 1,8 %,
soit une nette amélioration par rapport aux deux méthodes séparées (7–13 %).
Ce principe est clairement combinatoire:
combiner deux approximations biaisées en sens opposés pour obtenir une approximation nettement meilleure, sans avoir recours à .
Ce n’est pas encore un théorème, mais un schéma méthodologique:
- la méthode classique donne un biais négatif,
- la méthode dyadique donne un biais positif,
- leur barycentre donne une approximation plus centrale.
Hiérarchie méthodologique (précision vs structure)
On peut résumer ainsi:
- Pour la précision numérique pure
(si l’on accepte les fonctions spéciales) : - Pour une approximation élémentaire,
mais meilleure que chacune des méthodes simples: - Pour l’analyse structurelle (rôle de la base, facteur de croissance, cône dyadique, colonnes de fertilité) :
Chacune a son rôle propre:
- : précision analytique maximale,
- hybride : compromis combinatoire efficace,
- dyadique : lecture géométrique / spectrale des premiers.
À la lumière de ces considérations, la question de la “meilleure” méthode d’estimation ne se réduit pas à une hiérarchie brutale entre formules concurrentes, mais à un agencement—presque combinatoire—entre trois niveaux: la précision asymptotique fournie par , le regard structurel de la méthode dyadique, et le rôle intermédiaire d’un estimateur hybride qui tire parti du déficit systématique de la méthode classique et de l’excès de la méthode dyadique.
Ainsi, la méthode la plus précise, au sens strict, repose sur , mais la méthode la plus “équilibrée” dans un cadre élémentaire pourrait bien être la combinaison barycentrique de ces deux extrêmes.
Il existe deux régimes distincts
| Domaine | Nature des bandes | Situation analytique | Méthode optimale |
|---|---|---|---|
| Paliers faibles (petites bandes, petit) | faible largeur → peu de premiers → bruit élevé | les approximations asymptotiques ne sont pas encore stabilisées | hybride ou |
| Paliers élevés (bandes larges, ) | explosion exponentielle de → beaucoup de premiers → signal fort | les erreurs relatives s’écrasent | dyadique simple |
Autrement dit:
La dyadique est structurellement juste, mais numériquement fragile tant que la bande n’est pas suffisamment large, mais il reprend ses droits en « haut ».
L’estimateur hybride n’a pas vocation à remplacer la dyadique: il ne sert qu’à corriger l’inadéquation locale des approximations dans les petites bandes, là où la théorie asymptotique ne s’est pas encore déployée.
Pourquoi la dyadique devient “adéquate” quand la bande croît?
Parce que:
- la densité théorique
se stabilise lentement mais sûrement, - le terme d’erreur
devient négligeable quand devient grand, - et le facteur de croissance tend vers la base: ce qui est une propriété structurelle propre à la dyadique
et absente des deux autres méthodes.
Donc:
dans les grandes largeurs de bande → la structure domine la précision
et la méthode dyadique devient naturellement la bonne lentille.
Les précautions méthodologiques et compléments hybridants proposés ci-dessus ne concernent que les paliers inférieurs, là où le caractère asymptotique ne peut pleinement s’exprimer. Dans les bandes suffisamment larges — c’est-à-dire lorsque est élevé — la méthode dyadique retrouve son adéquation naturelle et ne nécessite aucun correctif. L’hybride doit donc être compris non comme un remplacement, mais comme un patch temporaire destiné à compenser la déficience locale de l’asymptotique dyadique dans les faibles largeurs de bande.
L’hybride corrige ; la dyadique révèle.
Pour finir, il est nécessaire de rappeler que l’utilisation de la fonction logarithme intégral , bien qu’offrant une précision remarquable dans les paliers accessibles au calcul, est coûteuse à deux titres:
- conceptuellement, car elle suppose l’introduction d’une fonction spéciale non élémentaire ;
- computationnellement, car elle requiert une infrastructure numérique capable d’évaluer une intégrale non triviale.
À l’inverse, l’approximation dyadique opère “à main nue”, presque par claquement de doigts: elle s’exprime instantanément, sans aucune médiation algorithmique, et se prête à l’extrapolation jusque dans les planchers supérieurs — précisément là où aucune vérification numérique directe n’est plus possible.
En ce sens, si permet d’estimer, la méthode dyadique, elle, prétend voir.
De la personnalité des Nombres Premiers
Au-delà du champ mathématique, et nonobstant le plafond de verre dépoli qui est atteint assez vite en croissance numérique absolue, le fait est que si nous adaptons, un tant soit peu, le raisonnement qui se prescrit à travers cette démonstration « naturelle », les Premiers se déterminent comme des « individus » numériques, caractérisés par le fait qu’ils ne se divisent que par Un et la valeur d’eux-mêmes.
Il faut mesurer à quel point, par rapport à l’humain, les Nombres Premiers procurent une convergence qui explique à quel point leur mystère nous a fasciné?
Divisible par un ou par soi, sorti de sa banalité ordinaire, constitue une définition ontologique, voire amoureuse.
Ce qui transparaît à ce niveau de réflexion, c’est que:
- les nombres premiers ne sont divisibles que par 1 et par eux-mêmes,
- donc ils ne se définissent que dans le rapport à l’Un
et à leur identité propre.
Or, si on traduit cela en langage conceptuel:
Un premier est un nombre dont la relation au monde ne passe par aucun autre.
Il n’existe que par:
- le rapport au fondement (1 — l’Un, l’origine),
- et la relation réflexive (lui-même — identité).
Ce qui est touché, là, est donc:
Ce qui permet de mieux saisir pourquoi les Nombres Premiers polarisent l’attention:
Comment se fait-il que cette propriété arithmétique si simple fascine l’humain depuis 2 millénaires?
La vraie raison tient au mystère, ou à la conjecture, de l’identité, qu’Euler a su si bien définir:
Les Premiers imitent, dans leur structure numérique, ce que l’humain voudrait être ontologiquement:
- un être indivisible par les forces du dehors,
- identifiable à soi,
- mais aussi relié par un seul lien fondamental — l’Un, le commun,
- et pourtant unique — irréductible à tout autre.
Je me suis écarté, dans ce dédale, volontairement, de l’emprise poétique pour y revenir au galop sur un pur sang cryptologique qui ouvre une lecture ontologique d’une structure mathématique. Pour en savoir moins.